If we accept that a square puzzle can't be tiled completely
by different squares...
How can we cover as much as possible of the square puzzle surface?
Of course we prefer a perfect fit, but this seems impossible with smaller puzzles (below 110 x 110).
In the beginning we hardly believed this could be such a big problem.
It turned out to be one of the thoughest mathemetical jigsaw puzzles we met!
Who can solve it?
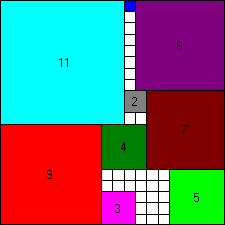
The three of us have puzzled and programmed on this isue with a lot of pleasure:
- Ed van Eersel
- Bart te Molder
- Pascal Huybers
This hobby started with a programming contest by Prospero,
but the original idea is much older. We found a perfect solution (no open space!) of the puzzle of 175 in a
book issued in 1956. This has been a great thinking job! They found it (and some perfect rectangles) by using mathematical graphs.
Our algorithm is a special type of
backtracking : depth-first traversal.
This means that we always first try a square on every possible place, before we replace it for a smaller square.
We believe the current super computers (using backtracking algorithms)
are still not able to solve the 175 puzzle within 10 years, but we challenge you to find a better algorithm.
Interesting questions:
- What is the smallest perfect solution? Probably N = 110 there are even three solutions!
- What is the largest square that can't be tiled perfectly?
- What relation does this puzzle have with fibonacci?
- In most solutions, the largest piece is placed in the corner.
Is this always the case? No, it isn't! For N = 73 and 87 the largest piece is at the middle of the edge.
Does there exist a solution where the largest piece is placed somewhere in the middle of the puzzle?
Yes, it exists! E.g. for N = 506.
Our solutions :
If you know something more (or just interested) you are welcome to contact us, mail to:

