Hoe kan je een vierkant puzzelvlak volledig opvullen met VERSCHILLENDE kleinere vierkanten?
Dat klinkt eenvoudig, en hoewel we oplossingen van anderen kenden (zelfs uit 1956!) duurde het
meer dan 15 jaar voordat wij onze eerste oplossingen vonden.
Door te beginnen met imperfecte vierkanten, verwachtten we de perfecte vanzelf tegen te komen.
We zijn daarmee nog niet verder dan 104x104, de rekentijd neemt steeds meer toe.
Via de perfecte rechthoeken lukte dit sneller, dat algoritme is veel efficienter voor dit doel.
Voordat we ze zelf vonden, wisten we van het bestaan van de perfecte vierkanten van o.a.
110, 112, 120, 139, 140, ..., 175, ... er bestaan er waarschijnlijk oneindig!
Alleen de getoonde oplossingen hebben we zelf met backtracking gevonden.
Onze algoritmes en/of computers zijn nog te langzaam voor de grotere puzzels.
110 is waarschijnlijk de kleinst mogelijke oplossing.
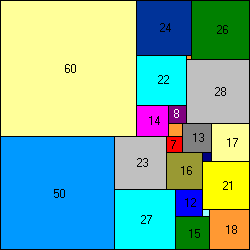 110x110 puzzel, 22 vierkantjes.
110x110 puzzel, 22 vierkantjes.
 110x110 puzzel, ook met 22 vierkantjes.
110x110 puzzel, ook met 22 vierkantjes.
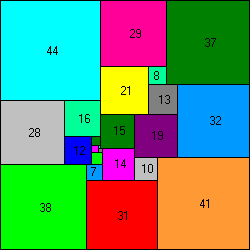 110x110 puzzel, met 23 vierkantjes.
110x110 puzzel, met 23 vierkantjes.
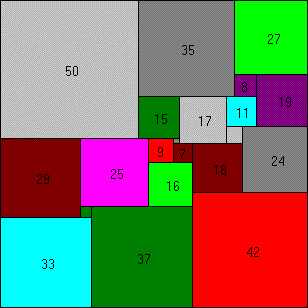 112x112 puzzel, met 21 vierkantjes.
112x112 puzzel, met 21 vierkantjes.
Deze vier zijn de enige die wij tot nu toe gevonden hebben. Het is door anderen aangetoond dat een perfecte oplossing minimaal 21 vierkanten heeft, daarvan is slechts ��n oplossing bekend! Dat is een redelijke indicatie dat het aardige moeite kost om er eentje met de hand op te lossen. Als je er meer wil zien kun je onderstaande de links volgen.