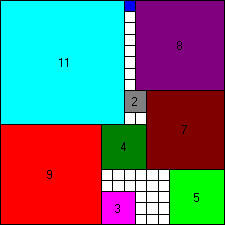
Het is de kunst om zoveel mogelijk oppervlak van het vierkante puzzelvlak met
verschillende vierkante stukjes te bedekken.
Ideaal is volledig opvullen, maar dit kan alleen bij grotere puzzels (groter dan 100 x 100).
Dat konden we ons aanvankelijk niet voorstellen, ofwel ... de ultieme uitdaging!
Wij hebben hier met zijn drie�n met erg veel plezier aan gepuzzeld en geprogrammeerd:
- Ed van Eersel
- Bart te Molder
- Pascal Huybers
We zijn met het programmeren hiervan begonnen naar aanleiding van een
programmeerwedstrijd van Prospero, en daarna nog lang doorgegaan.
Het oorspronkelijke puzzelidee is al veel ouder,
we vonden een perfecte oplossing van de puzzel van 175 bij 175 in een boek uit 1956.
Dat was noest handwerk! Gevonden met behulp van grafen (soort wiskundige netwerken).
Ons gebruikte algoritme is een variant van
backtracking : namelijk depth-first traversal.
Dat houdt in dat je een vierkant eerst op alle plaatsen uitprobeert en pas als dat klaar is
het vierkant vervangt voor een andere.
Interessante vragen:
- Wat is de kleinste perfecte oplossing? Waarschijnlijk N = 110 daar zijn er zelfs drie van!
- Wat is de grootste puzzel zonder perfecte oplossing?
Hier zullen we misschien nooit een antwoord op krijgen, er bestaat misschien altijd een grotere.
- Wat heeft deze puzzel met fibonacci te maken?
- Bij de meeste puzzels staat het grootste vierkant in de hoek.
Bestaan er uitzonderingen? Ja! Bij N = 73 en 87 staat de grootste midden aan de rand
Bestaat er een oplossing waarbij het grootste vierkant ergens in het midden staat?
Ja, zo'n oplossing bestaat! B.v. bij N = 506.
Onze oplossingen:
Als je meer over deze puzzel weet, andere oplossingen dan ons hebt,
of hier gewoon mee bezig geweest bent, dan horen we graag je ervaringen!
Mail naar:

