I would easily think: 'Puzzles with square pieces must be dead simple, you're quickly bored'. You can rotate a square, but it will remain the same square.
Suppose you have a rectangular room and all different square tiles for the floor... How can you tile your floor without using the saw?
It turned out to be a bit less easy than expected!

1) Only concrete sizes of squares are available, e.g. centimeters or inches, or use square paper.
2) The puzzle surface is square or rectangular, say 6 x 6 to start with.
3) The pieces are all squares, smaller than the short side of the rectangle, in this case 1 x 1 up to 5 x 5.
4) You may decide yourself which pieces to use and which not, as long as they are all different.
And now right on ... of course pieces may not overlap.

You can easily conclude: this is an infinit number of jigsaw puzzles and you can find out that each is really different!
The larger the puzzle surfice, the more possibilities and tougher the puzzle.

A) Imperfect squares

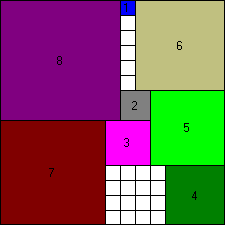15x15 puzzle

Target is to leave as few open space as possible (none if possible).
Better solutions often go with the larger puzzles.
If you can cover the complete square you found a Perfect Square.

B) Perfect rectangles

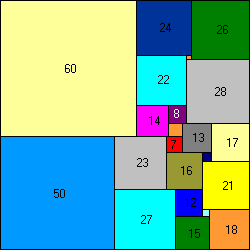
65x47 puzzle

Searching for rectangles which can be filled perfectly with different squares.
There is a surprising connection to the Fibonacci numbers!

C) Perfect squares

Perfect squares are of course the ultimate challenge. How to fill a square with different square pieces?